Derivadas de orden superior
Lo mismo que sucede con las derivadas ordinarias, es posible encontrar derivadas parciales de una función de varias variables de órdenes segundo, tercero y superiores, supuesto que tales derivadas existen. Denotamos las derivadas de orden superior por su orden de derivación. Por ejemplo, hay cuatro formas distintas de encontrar una derivada parcial segunda de z=f(x,y).
1. Derivar dos veces respecto de x:
2. Derivar dos veces respecto de y:
3. Derivar primero con respecto a x y luego con respecto a
y:
4. Derivar primero con respecto a y y luego con respecto a
x:
Los casos tercero y cuarto se conocen como derivadas
parciales cruzadas. Se debe observar que hay tipos de notación para las
derivadas parciales cruzadas, según convenio se utilice para indicar el orden
de derivación. Así, la parcial
orden
de derecha a izquierda indica que la primera derivación es con respecto a x, pero
la parcial
(fy)x=fyx Orden de izquierda a derecha indica que la primera derivación es con respecto a y.
Observar que con ambas notaciones se deriva primero respecto de la variable que
está más cercana a f. Ademas recordemos que si la función es continua y sus derivadas parciales de primer orden son continuas entonces, sus derivadas parciales cruzadas van hacer iguales.
-Haciendo uso de las derivadas de orden superior en clases demostramos las ecuaciones unidimensional y bidimensional del calor.
-Ademas decimos que es armónica si satisface la ecuación de Lanplace.
Zxx+Zyy=0
Incrementos totales y parciales
En R*R
El incremento Δx de una variable x es el aumento o disminución que experimenta, desde un valor x = x0 a otro x = x1 de su campo de variación. Así, pues,
Δy = f(x+Δx) - f(x)
Δx = x1 – x0 o bien x1 = x0 + Δx
En R*R*R z = f(x,y)
ΔZx = f(x+Δx,y) - f(x,y)
ΔZy = f(x,y+Δy) - f(x,y)
ΔZ = f(x+Δx,y+Δy) - f(x,y)
ΔZ ≠ ΔZx + ΔZy
Generalizando, si los incrementos tienden a cero se hacen diferenciales por lo que dedudimos la siguiente forma:

Duf(x , y) = ∇ f(x , y) . u(unitario)
Duf(x , y) =∇ f(x , y) . u = |∇f ||u| cos β y si |u|=11)Cuando el vector unitario y el gradiente forman un β=0, se dará una optimizacion máxima igual a:
Duf(x , y) = |∇f |
2) Cuando el vector unitario y el gradiente forman un β=90, es decir son ortogonales o perpendiculares, se da el estado estacionario.
Duf(x , y) = 0
3) Cuando el vector unitario y el gradiente forman un β=180, el vector direccional disminuirá en esa dirección dándose el mínimo valor.
Duf(x , y) = -|∇f |
1)Máximos y mínimos absolutos.
2)Máximos y mínimos condicionados.
Multiplicadores de Lagrange.
3)Máximos y mínimos relativos.
Nota:En integrales dobles sobre rectángulos la función es simétrica respecto a sus variables y es indiferente el orden de las integrales iteradas.
3) Cuando el vector unitario y el gradiente forman un β=180, el vector direccional disminuirá en esa dirección dándose el mínimo valor.
Duf(x , y) = -|∇f |
Regla de la cadena para dos variables
Derivación de funciones implícitas
-Se puede realizar por tres métodos:
1)Por diferenciación.
2)Por derivación implícita.
3)Determinante Jacobiano.
Máximos y mínimos
1)Máximos y mínimos absolutos.
2)Máximos y mínimos condicionados.
Multiplicadores de Lagrange.
3)Máximos y mínimos relativos.
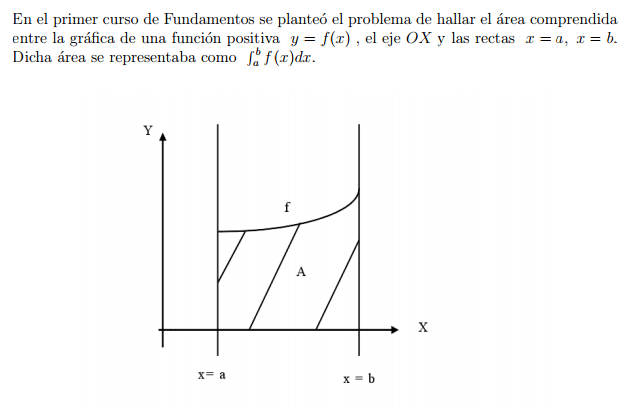
Integrales múltiples
Introducción
Integral doble
Integral triple
Integrales sobre regiones rectangulares
Integración sobre regiones mas generales
Transformación de integrales múltiples
-Vimos ejercicios sobre integrales dobles , triples y la transformación de coordenadas esféricas, cilíndricas y cartesianas en el determinante jacobiano.
-Calculo de volúmenes.
-Calculo de masa.
*Discreta
*Continua















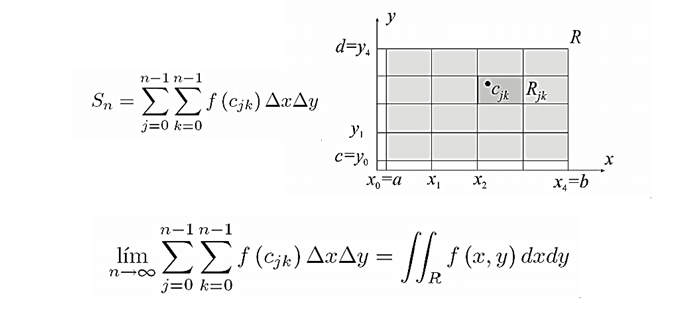



No hay comentarios:
Publicar un comentario